Summary
- Easy negative sample에 대한 학습 weight를 줄이고, hard negative sample에 대한 weight를 늘리는 것으로 클래스 불균형 현상을 해결하는 cross entropy loss의 확장판.
- 최초의 제안은 one-stage object detection 성능 향상을 위함.
$FocalLoss(p_{t}) = -\alpha t(1-p_t)^{\gamma}log(p_t)$
참고논문: https://arxiv.org/pdf/1708.02002
Cross entropy loss
많은 분야에서 사용하고 있는 cross entropy loss는 그 유용성을 증명하였지만, 잘 분류한 경우보다 잘못 예측한 경우에 대하여 페널티를 부여하는 것에 초점을 두는 단점이 있다 . 예를 들어, 이진 분류에서 예측한 확률을 p, 실제 라벨 값을 y라고 가정하면 아래와 같은 식이 성립된다.
$Cross Entropy Loss(p,y) = -y log(p) - (1-y) log(1-p)$
위 식에서 y 값이 1인경우를 예시로 들면 아래와 같다.
$Cross Entropy Loss(p,y) = - log(p) + 0 = - log(p)$
만약 p의 값이 1이면 최종적인 loss 값은 0이 되는데, 잘 예측 하였지만, 보상이 없는 경우다.
만약 p의 값이 0에 가까운 값이면 최종적인 loss 값은 무한에 가까운 값이 되는데, 패널티가 매우 커지는 경우다.
또한 클래스 불균형에 대해 굉장히 민감한데, foreground 인 경우를 p=0.95, y=1이라고 가정하고 background 인 경우를 p=0.05, y=0이라고 가정해보자.
$Cross Entropy Loss(foreground) = - log(0.95) = 0.05$
$Cross Entropy Loss(background) = - log(1-0.05) = 0.05$
위 식을 보면 문제가 없어보이지만, foreground 케이스와 background 케이스 모두 같은 loss 값을 가진다는 큰 문제가 있다. 이는 background 케이스의 수가 훨씬 더 많기 때문에, 같은 비율로 loss 값이 업데이트되면 background 케이스에 대한 학습이 많이 진행 될 것이고 이 작업이 누적되면 foreground에 대한 학습량이 현저히 줄어들기 때문이다.
Balanced cross entropy loss
클래스 불균형 문제를 해결하기 위해 weight를 추가로 곱하는 balanced cross entropy loss가 제안되었다. weight는 클래스 수 각각의 역수의 개수를 의미하고, $𝑤_𝑡$ ≤ 1 의 범위의 값을 사용한다. 식은 아래와 같다.
$Balanced Cross Entropy Loss = - w_t log(p_t)$
Balanced Cross Entropy Loss의 weight에 대한 값의 조절을 통해 클래스 불균형문제를 해결할 수 있을 것으로 보이지만 한계점이 있다. Easy/Hard example 구분을 할 수 없다는 점인데, 단순히 갯수가 많다고 Easy라고 판단하거나 Hard라고 판단하는 것에는 오차가 발생할 수 있다.
Focal loss
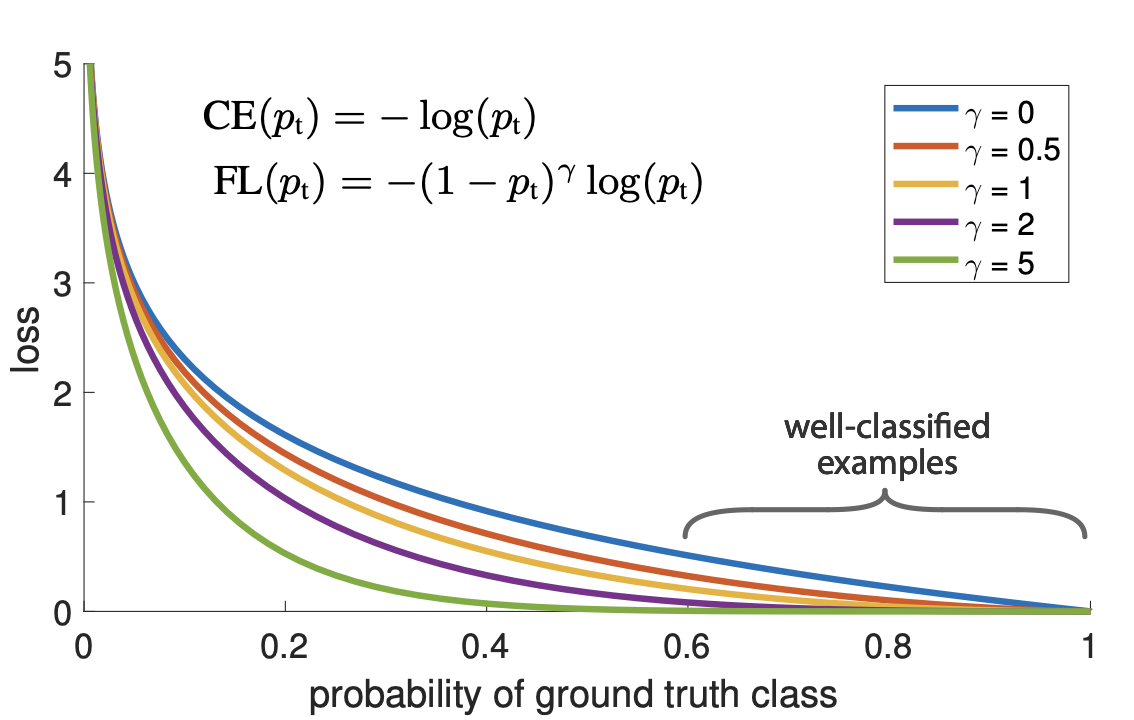
Focal Loss는 easy sample의 weight를 줄이고 hard negative sample에 대한 학습에 초점을 맞추는 cross entropy loss 함수의 확장판이라고 말할 수 있다. cross entropy loss 대비 loss에 $(1-p_t)^\gamma$ 항을 곱하고, 전체적인 loss 값을 조절하는 $\alpha$ 값 또한 논문에서 사용되었다. 각각의 값은 2, 0.25로 설정하며 수식은 아래와 같다.
$FL(p_{t})=-\alpha t(1-p_t)^{\gamma}log(p_t)$
만약, 모델이 잘못 분류한 경우 $p_t$가 작아지게 되고 동시에 $1-p_t^{\gamma}$ 와 $log(p_t)$가 동시에 커져서 Loss에 반영된다. 반대로 $p_t$가 1에 가까워 지면 $1-p_t^{\gamma}$는 0에 가까워지고 cross entropy loss와 동일하게 $log(p_t)$의 값 또한 줄어들게 된다. 여기서 $\gamma$를 focusing parameter라고 하며, 이는 easy example에 대한 loss의 비중을 낮추는 역할을 한다. 이를 통해 easy negative 케이스에 대해 loss가 누적되며 발생하는 불균형 문제를 개선하였다.
'딥러닝 이론 > BasicML' 카테고리의 다른 글
| 공변량(convariate) (0) | 2024.05.09 |
|---|---|
| Univariate time series (0) | 2024.05.09 |
| L1 Norm, L2 Norm, L1 Loss, L2 Loss 차이점 (0) | 2023.11.10 |
| Coarse-grained classification과 Fine-grained classification (0) | 2023.10.30 |
| Concept shift (0) | 2023.10.26 |

